Time, Ratio of Emissions to GDP, and Countries and Their Relationship with CO2 Emissions

Serena Bohra (Data Science at Reed College)https://reed-statistics.github.io/math241-spring2022/ , Tina Qin (Data Science at Reed College)https://reed-statistics.github.io/math241-spring2022/
May 4, 2022

Introduction

Greenhouse gas emissions are gas emissions caused by human activities; for example, carbon dioxide emits from burning fossil fuels for electricity and transportation (Sources of Greenhouse Gas Emissions, n.d.). Such emissions strengthen the greenhouse effect, which then results in climate change. Since the start of the industrial revolution from the mid-18th century to about 1830, the increase of industrial activities gradually led to the warming up of the climate system on Earth, and to this day, climate change has become a growing concern (Industrial Revolution, 2022; Tiseo, 2021).

In this project, we aim to look at some variables related to greenhouse gas emissions and observe if there is any relationship between them. Specifically, we want to investigate the significance of the relationship between a country’s GDP per capita and its CO2 emissions, and the significance of the relationship between time and CO2 emissions for a multitude of countries.

To achieve this, we found the Emissions data set, a CSV file from the CORGIS Dataset Project, about greenhouse gas emissions by country (Kafura, 2019). The data file from the CORGIS Dataset Project is originally obtained from the Emissions Database for Global Atmospheric Research database. It includes 8385 observations and 12 variables: country, year (1970-2012), and variables related to gas emissions, which are

  1. emissions of: CO2 (carbon dioxide), N2O (nitrous oxide), and CH4 (methane);
  2. emissions from: the power industry, the infrastructure of buildings, means of transportation, other industrial combustion, and other sectors;
  3. the ratio of: greenhouse gas emissions per $1,000 of GDP, and emissions each person.

All variables above are numeric, either measuring emission or ratio. Emissions of CO2 are measured in kilotons, and all others are measured in equivalent kilotons of CO2.

Methods and Results

Time, GDP, and CO2 Emissions

The first observation is between time and CO2 emissions. Time will be measured in the years from 1970 to 2012, and CO2 emissions will be expressed as the greenhouse gasses emitted through human activities measured in kilotons. The country of the Maldives will be used as a control variable for the first two data explorations. The Maldives was chosen out of interest because in the time period of 2001-2020, the Maldives experienced a vast amount of deforestation and a significant loss of tree cover (Statistics about Forests in Maldives, n.d.). We became intrigued to investigate the CO2 emissions of kilotons in the Maldives over time.

hide 
# load package
library(tidyverse)

# read csv file and rename variables
emissions <- read_csv("emissions.csv")
names(emissions) <- c("country", "year", "CO2", "N2O", "CH4", "power_ind", 
                      "buildings", "transport", "other_ind", "other_sect", 
                      "ratio_per_GDP", "ratio_per_capita")
hide 
# plot of CO2 emissions by year in the Maldives
emissions %>% 
  filter(country == "Maldives") %>% 
ggplot(aes(x = year, y = CO2)) + 
  geom_point() + 
  labs(x = "Year", 
       y = "CO2 Emissions (kilotons)",
       title = "CO2 Emissions over the Years for the Maldives" )

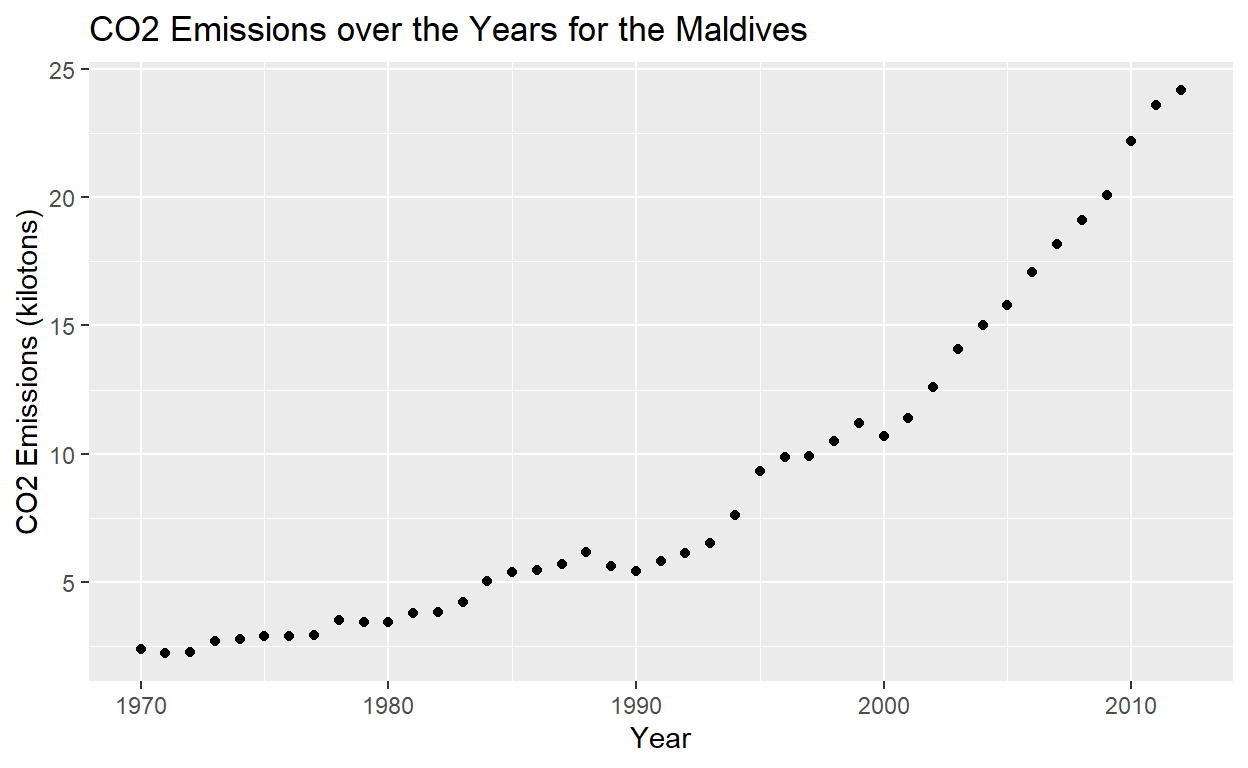
When initially looking at the graph, we noticed that as time increased, so did the CO2 emissions; the CO2 emissions were increasing exponentially. There was a significant increase in CO2 emissions in the later years. This aroused our interest to find out if there was a significant reason why this had occurred, such as, if there was an increase in some factor that related to CO2 emissions. An increase in factory farming increases the emission of several greenhouse gasses, and factory farming is related to economic development, so we decided to create a scatter plot to visualize the relationship between the ratio of emissions to GDP and CO2 emissions.

hide 
emissions %>% 
  filter(country == "Maldives") %>% 
ggplot(aes(x = ratio_per_GDP, y = CO2)) + 
  geom_point() + 
  labs(x = "Ratio of Emission to GDP", 
       y = "CO2 Emissions",
       title = "Relationship of Ratio of Emission to GDP and Emissions of CO2 for the Maldives")

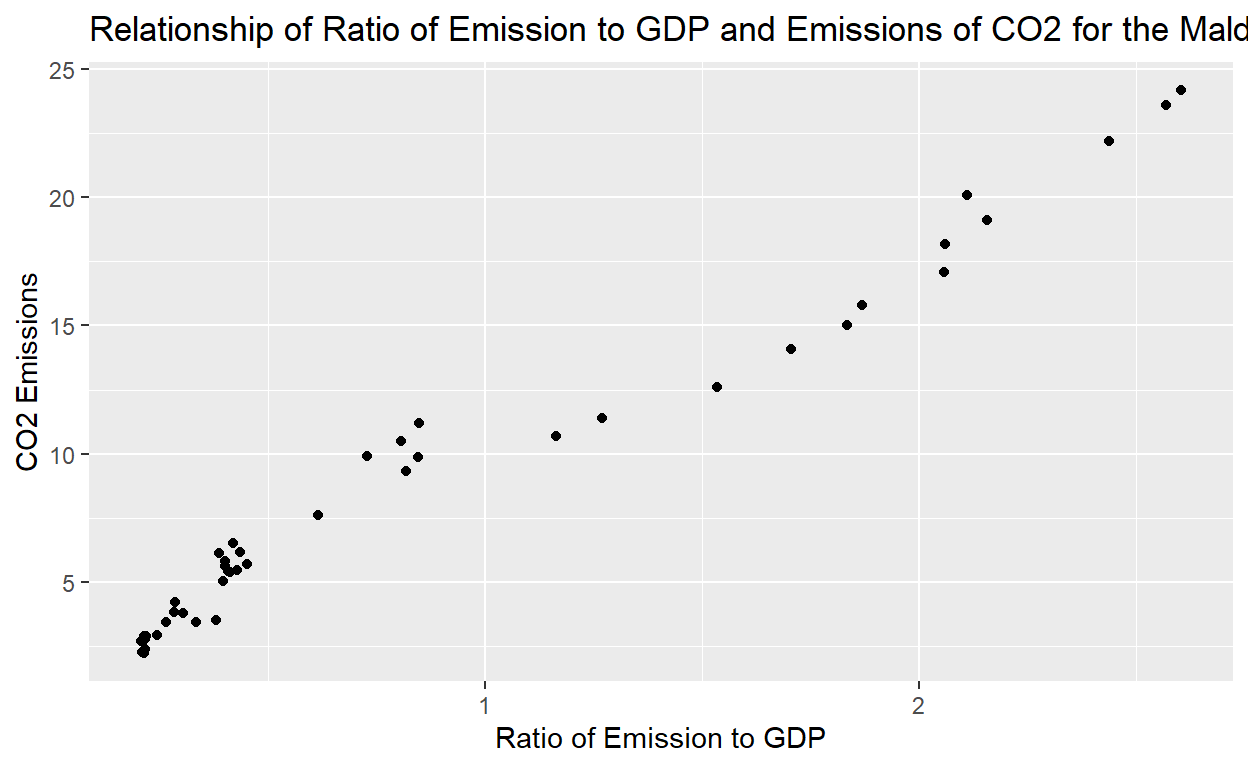
There is a positive association between the ratio of emissions to GDP and CO2 Emissions for the Maldives, and there were no significant outliers presented in the graph. In the next section, we will investigate if there was a significant relationship between these two variables.

Hypothesis Test about GDP and CO2 Emissions

First, we found the correlation between the ratio of emissions to GDP and CO2 emissions for the country of the Maldives.

hide 
emissions %>%
  filter(country == "Maldives") %>% 
  summarize(r_free = cor(ratio_per_GDP, CO2))

# A tibble: 1 × 1
  r_free
   <dbl>
1  0.985

Evidently, the correlation is very close to 1 which indicates a strong positive association between the two variables. Then we conducted a linear model hypothesis test to test and see if a linear model is appropriate for these variables. We stated the equation as \(y_{\text{CO}2} = \beta_0 + \beta_1x_{\text{GDP}}\), with \(y_{\text{CO}2}\) as the CO2 emissions response variable, \(\beta_0\) as the intercept, and \(\beta_1\) as the slope predicted by the null and alternate hypothesis.

\(H_0\): There is no linear relationship between the ratio of emissions to GDP and CO2 emissions for the country of the Maldives. The expected slope of the linear model is \(\beta_1 = 0\).

\(H_1\): There is a linear relationship between the ratio of emissions to GDP and CO2 emissions for the country of the Maldives. The expected slope of the linear model is \(\beta_1 \neq 0\).

hide 
emissions %>% 
  filter(country == "Maldives") %>% 
  lm(CO2 ~ ratio_per_GDP, data = .) %>% 
  summary()


Call:
lm(formula = CO2 ~ ratio_per_GDP, data = .)

Residuals:
    Min      1Q  Median      3Q     Max 
-1.7224 -0.7504 -0.2121  0.8579  2.5467 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)     1.6989     0.2593   6.552 7.09e-08 ***
ratio_per_GDP   8.1951     0.2226  36.813  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.117 on 41 degrees of freedom
Multiple R-squared:  0.9706,    Adjusted R-squared:  0.9699 
F-statistic:  1355 on 1 and 41 DF,  p-value: < 2.2e-16

The multiple R-squared value was also very close to 1 which signifies that the proportion of variability that the linear model is 0.976. Additionally, the p-value was also very close to 0 which indicates that there is strong evidence against the null hypothesis, thus indicating that a linear model is an appropriate fit for the variables of GDP and CO2 emissions for the country of the Maldives. Based on the results presented, as the GDP increases by one unit, the CO2 emissions in the Maldives increases by 8.1951 units.

Time and CO2 Emissions for Multiple Countries

We examined which countries have the highest average CO2 emissions and how the CO2 emission changed over the years. This value was calculated by taking an average of the CO2 emissions of each country over the years.

hide 
emissions %>% group_by(country) %>%
  summarize(avg_CO2 = mean(CO2)) %>%
  arrange(desc(avg_CO2)) %>%
  head(25) %>%
  ggplot(aes(x = avg_CO2, y = reorder(country, avg_CO2))) + 
    geom_bar(stat = "identity") +
    labs(title = "Top Countries by Highest Average CO2 Emissions",
         x = "Average CO2 Emission", y = "Country")

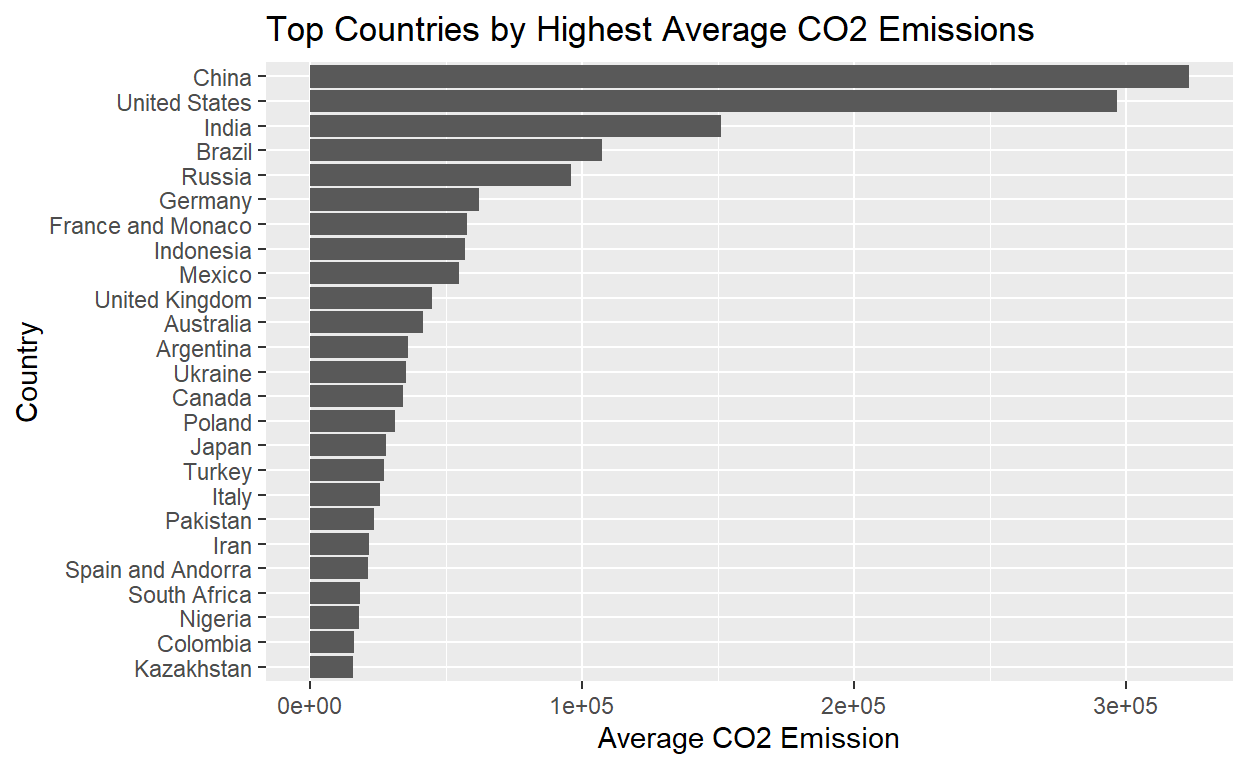
As the bar plot shows, China, United States, India, Brazil, and Russia are the top 5 countries with the highest CO2 emissions through the years. China and United States have especially high emission. Then the next plot compares the change of emissions overtime of these top 5 countries.

hide 
emissions %>% filter(country %in% c("China", "United States", "India", "Brazil", "Russia")) %>%
  ggplot(aes(x = year, y = CO2, color = country)) +
    geom_line() +
    labs(title = "Change of CO2 Emissions Overtime in the Top 5 Countries by Average CO2 Emission",
         x = "Year", y = "CO2 Emission")

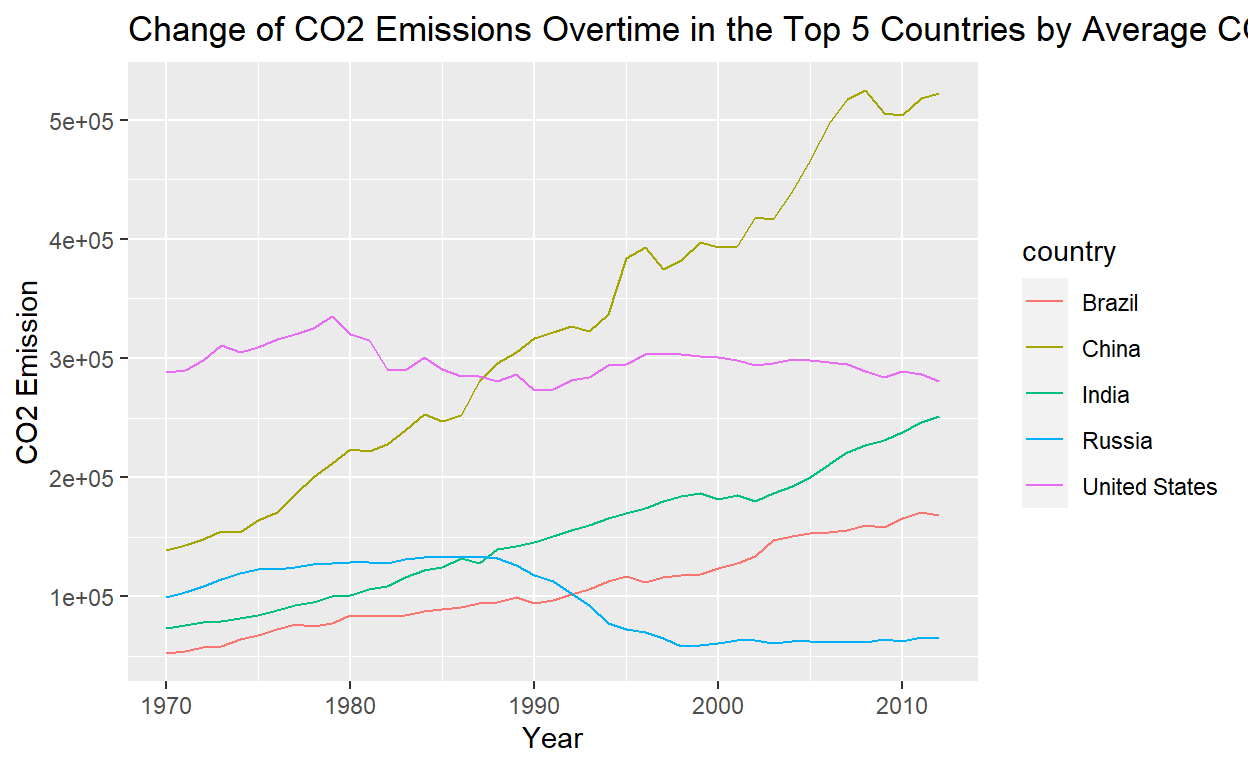
In the time period after 1985 and around 1990, we see multiple crossovers: between United States and China, Russia and India, and Russia and Brazil. The trends in China, India, and Brazil are increasing, while the trends in United States and Russia are slightly decreasing. This could be due to the increase in the amount of factories and industries in the developing countries and a relatively stable trend in the developed countries.

To fit a model to predict CO2, we used multiple linear regression covariating the variables of emissions from all the industries. That is, we want to predict the significance of the coefficients of the formula \(y_{\text{CO}2} = \beta_0 + \sum{\beta_ix_i}\), where \(x_i\) are variables of emissions from power industries, buildings, transportation, other industries, and other sectors. Since these variables are all measured in equivalent kilotons of CO2, it is expected that all variables will be significant. Indeed, the low p-values show that they are all significant predictors.

hide 
summary(lm(CO2 ~ power_ind + buildings + transport + other_ind + other_sect, emissions))


Call:
lm(formula = CO2 ~ power_ind + buildings + transport + other_ind + 
    other_sect, data = emissions)

Residuals:
    Min      1Q  Median      3Q     Max 
-176806   -2115   -1750    -107  148119 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 2108.903    155.396   13.57   <2e-16 ***
power_ind    -45.331      3.772  -12.02   <2e-16 ***
buildings    198.794      6.436   30.89   <2e-16 ***
transport     68.067      4.883   13.94   <2e-16 ***
other_ind     94.355      5.467   17.26   <2e-16 ***
other_sect   254.433     14.187   17.93   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 13570 on 8379 degrees of freedom
Multiple R-squared:  0.8651,    Adjusted R-squared:  0.865 
F-statistic: 1.074e+04 on 5 and 8379 DF,  p-value: < 2.2e-16

We then conducted the same method using the same variable but predicting the N2O emissions.

hide 
summary(lm(N2O ~ power_ind + buildings + transport + other_ind + other_sect, emissions))


Call:
lm(formula = N2O ~ power_ind + buildings + transport + other_ind + 
    other_sect, data = emissions)

Residuals:
    Min      1Q  Median      3Q     Max 
-600241   -8153   -7173   -2395  613738 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 8160.426    647.054  12.612  < 2e-16 ***
power_ind   -213.827     15.707 -13.614  < 2e-16 ***
buildings    937.241     26.798  34.974  < 2e-16 ***
transport     -2.084     20.334  -0.102  0.91837    
other_ind     65.746     22.764   2.888  0.00389 ** 
other_sect  1433.964     59.075  24.274  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 56500 on 8379 degrees of freedom
Multiple R-squared:  0.7657,    Adjusted R-squared:  0.7656 
F-statistic:  5477 on 5 and 8379 DF,  p-value: < 2.2e-16

In this model, the p-values for emissions from transportation and other industries are larger than others and larger than the previous model for CO2, with the one for transportation especially high. So the emissions from means of transportation is not a statistically significant predictor for N2O emissions.

Conclusions

The main objectives of this project were to investigate the significance of the relationship between GDP per Capita and CO2 emissions for the country of the Maldives as well as to investigate the significance of the relationship between time and CO2 emissions for a variety of countries. Our findings suggested that there is a significant linear relationship between the GDP per Capita and CO2 emissions for the Maldives, and that emissions from transportation are not a significant predictor for N2O emissions. If we had more time and resources for further research, we could have investigated other types of emissions in the Maldives such as methane and nitrous oxide for more insightful conclusions. Additionally, this project solely focused as GDP per Capita as an explanatory variable. With more time, this project could have focused more on other explanatory variables that were present in the data set such as power industries, infrastructure, and transportation.

Class Peer Reviews

Industrial revolution. (2022). Britannica. https://www.britannica.com/event/Industrial-Revolution
Kafura, D. (2019). Emissions CSV file. CORGIS Dataset Project. https://corgis-edu.github.io/corgis/csv/emissions/
Sources of greenhouse gas emissions. (n.d.). United States Environmental Protection Agency. https://www.epa.gov/ghgemissions/sources-greenhouse-gas-emissions
Statistics about forests in maldives. (n.d.). Global Forest Watch. https://tinyurl.com/32nnbff3
Tiseo, I. (2021). Historical carbon dioxide emissions from global fossil fuel combustion and industrial processes from 1750 to 2020. Statista. https://www.statista.com/statistics/264699/worldwide-co2-emissions/#:~:text=The%20carbon%20dioxide%20emissions%20released,billion%20metric%20tons%20of%20CO2

References

Reuse

Text and figures are licensed under Creative Commons Attribution CC BY 4.0. The figures that have been reused from other sources don't fall under this license and can be recognized by a note in their caption: "Figure from ...".