Missed Class

If you are unable to attend class, you can still earn participation credit by completing the following activity:

  1. Watch the day’s lecture video (which will usually be posted by around 3pm PST).

  2. Write a short response to the video that includes:

    1. A 1 - 2 paragraph summary of the main ideas and topics discussed.

    2. A 1 - 2 paragraph discussion of 1 real-world example of the theory, method or application in the lecture that has pertinence to your life, or was in the news, or that you’ve found interesting; for example, the lecture may have discussed the decomposition of an image using the grammar of graphics, and you could find one image from a newsroom and discuss the geommetric shapes, aesthetic attributes, and data variables that appear in this image.

    3. One question you have about the content covered in the lecture video.

  3. Send your response to Nate on Slack (either as a message or attached image / .pdf file) before the start of the next class day.

Week 1

Monday 1-24

Lecture Video (Reed Kerberus log-in required)

Reading Assignment

Note that the listed reading assignments should be completed prior to class

Homework Assigned

Homework is due by 11:59pm on Friday

Supplementary Material

  • Here is a link to the Tampa Bay Times article on race and the Stand Your Ground defense from which today’s data was taken.

  • Here is an article by Jeff Witmer, who did some analysis on the TBT data.

  • Here is a short video (~4 min) further discussing the statistical phenomenon of Simpson’s Paradox that we observed in class today.

Wednesday 1-26

Lecture Slides

Lecture Video

Topics

  • R and RStudio

  • Structure of Data

Reading Assignment

Note that the listed reading assignments should be completed prior to class

  • Read Sections 1.1 - 1.4 in ModernDive

  • Complete Learning Checks LC 1.4, LC 1.5, LC 1.6 and submit to Gradescope.

Due

Note that the listed assignments should be completed prior to class

  • Complete Slack Introduction:
    1. Sign-in to our Slack workspace
    2. Navigate to the #classroom-wells channel using the menu on the left side of the screen and post a message with your name and statistics that describe yourself, two of which are true and one of which is false (don’t say which is which). After at least 1 person has guessed, you can respond with the correct answer.
    3. Find another person’s post, hover over it, and click the chat bubble icon to start a thread. Then guess which of that person’s three statements is false.
    4. Finally, find my name (Nate Wells) under Direct Messages on the left side of the screen, and send me a private message answering the following questions:
      1. What is your preferred name? (and what are your pronouns, if you’d like to share?)
      2. Have you taken a statistics course previously?
      3. What do you hope to take away from this course?
      4. What concerns do you have about this course, or about academics in general this term?
      5. What is one image that best describes you? (feel free to upload it)

Supplementary Material

  • Here is complete Netflix dataset that was discussed in class today: Netflix.csv

  • This data set was obtained from the TidyTuesday project here.

  • TidyTuesday is a weekly data investigation project organized by a group of data scientists, with the purpose to practice and collaborate on data summarizing and arranging tasks.

Week 1 Lab

Topics

  • Introduction to R and RStudio

Lab Assignment

Labs are due by 11:59pm the day before your next lab meeting

Friday 1-28

Lecture Notes

Lecture Video

Topics

  • The Grammar of Graphics

Reading Assignment

Note that the listed reading assignments should be completed prior to class

  • Sections to Read Sections 2.1 and 2.2 in ModernDive

  • Reading Questions (Submit answers on Gradescope)

    1. Suppose you need to describe to someone else, who has never plotted points on a graph before, a general method for plotting several points on a graph (that is, by drawing them out by hand on a piece of paper). In a short paragraph, provide instructions for this person how to plot the points (1, 5), (2, 3), and (3, 5) on a piece of paper. (To reiterate, assume this person has never plotted before, so does not have a prior model to reference or imitate).

Homework Due

Homework is due by 11:59pm on Friday

Supplementary Material

  • An in-depth discussion of the graphical reasoning surrounding the Challenger disaster can be found in Edward Tufte’s booklet Visual and Statistical Thinking: Displays of Evidence for Making Decisions (available for check-out in the Reed library)

  • In 1986, President Reagan a presidential commission tasked with investigating the Space Shuttle Challenger distaster. Their findings were given in the Rogers Commission Report, and summarized in live congressional testimony.

    • One of the most famous moments of the congressional testimony was the demonstration by renowned physicist, Richard Feynman, of the failure of O-rings at low temperatures. Here is a 1-minute video clip of his demo.

Week 2

Monday 1-31

Note: Class will be held remotely on Zoom on Monday, 1-31. The zoom link is available in the #announcements-wells channel of our Slack workspace.

Lecture Notes

Lecture Video

Topics

  • Exploring ggplot2: Scatterplots, Linegraphs and more

Reading Assignment

Note that the listed reading assignments should be completed prior to class

  • Sections to Read Sections 2.3 - 2.5 in ModernDive

  • Reading Questions (Submit answers on Gradescope)

    1. Answer LC2.6, LC2.11, LC2.16 from the text

Wednesday 3-2

Lecture Notes

Lecture Video

Topics

  • ggplot2 continued: Histograms, Boxplots, Barcharts, and customization

Reading Assignment

Note that the listed reading assignments should be completed prior to class

  • Sections to Read Sections 2.6 - 2.9 in ModernDive

  • Reading Questions (Submit answers on Gradescope)

    1. Answer LC2.20, LC2.25, LC2.27 from the text

Supplementary Material

  • Portland Biketown is a bike-sharing system owned by the Portland Bureau of Transportation, managed by Lyft, and sponsored by Nike. The program allows uses to rent bikes at any station throughout the city, ride, and then deposite the bike at any station.

  • The biketown program logs data on each ride, including start/end location and time, disance traveled, fair type (subscriber vs casual), and more. The data is uplaoded to the program’s website and then made publically available here.

  • Here is a the biketown.csv file of a sample of 9999 observations that I’ve been using in class Monday and Wednesday.

Week 2 Lab

Lab Video

Topics

  • Graphics using ggplot2

Lab Assignment

Labs are due by 11:59pm the day before your next lab meeting

Friday 2-4

Lecture Notes

Lecture Video

Topics

  • Exploring categorical and quantitative variables using summary statistics.

Reading Assignment

Note that the listed reading assignments should be completed prior to class

  • Sections to Read Sections 4.1, 4.3, 5.2 - 5.5 in Introduction to Modern Statistics Note this is not the ModernDive textbook

  • Reading Questions (Submit answers on Gradescope)

    1. What are two different values that can be used to measure the center of a quantitative data set? What are two different values that can be used to measure the spread of a quantitative data set?

    2. True or false? You can compute the mean of a categorical variable. Explain.

Homework Due

Homework is due by 11:59pm on Friday

Week 3

Monday 2-7

Lecture Notes

Lecture Video

Topics

Supplementary Material

Here is an .Rmd file of solutionsto the day’s wrangling activity. And here is the output of the code.

Reading Assignment

Note that the listed reading assignments should be completed prior to class

  • Sections to Read Sections 3.1 - 3.6 in ModernDive

  • Reading Questions (Submit answers on Gradescope)

    1. What is one “problem” the pipe operator solves when coding?

    2. Answer LC3.2, LC3.6 from the text

Wednesday 2-9

Lecture Video

Topics

Reading Assignment

  • Sections to Read Sections 3.8, 3.9, 4.1, 4.2 in ModernDive

  • Reading Questions (Submit answers on Gradescope)

    1. Answer LC3.18, LC4.1 from the text

    2. In addition to reading questions, please complete this anonymous survey for use in Wednesday’s class. You do not need to submit the survey results to gradescope.

Supplementary Material

Here is an .Rmd file of solutionsto the day’s wrangling activity. And here is the output of the code.

Week 3 Lab

Demo Video

Topics

Lab Assignment

Friday 2-11

Lecture Video

Lecture Notes

Topics

  • Principles of Data Collection: samples, surveys, and experiments

Reading Assignment

  • Sections to Read Sections 2.1, 2.2 and 2.3 in Introduction to Modern Statistics

  • Reading Questions (Submit answers on Gradescope)

    1. The website Rotten Tomatoes shows a proportion of audience respondents who were satisfied with a film. If a particular film has an audience score of 50%, do you think this means that 50% of all audience members are dissatisfied with the film? Why or why not?

    2. For each of the following two research questions, what is the implied population and what represents an individual observation?

      1. Have daily high temperature readings increased in Portland, OR over the past 20 years?

      2. Does the Moderna COVID-19 vaccine reduce the death rate in patients with severe cases of COVID-19?

Homework Due

Homework is due by 11:59pm on Friday

Week 4

Monday 2-14

Lecture Notes

Lecture Video

Topics

  • Correlation, Causation, Experiments, and Observational Studies

Reading Assignment

Note that the listed reading assignments should be completed prior to class

  • Sections to Read Review Sections 2.1 - 2.3 in Introduction to Modern Statistics (this was also the same reading as last Friday). Then spend some time exploring the Gapminder Bubbles Charts

  • Reading Questions (Submit answers on Gradescope)

    1. On the Gapminder Bubbles Charts, change some of the variables on the x- and y-axes. What were some variables that seemed strongly correlated? Do you expect any of these variables to have a causal relationship? Explain.

    2. Describe one interesting trend or observation you discovered using the Gapminder bubble charts.

Wednesday 2-16

Lecture Notes

Lecture Video

  • Note that around the 30-minute mark, my laptop ran out of batteries, and so there is a slight time skip (~2 minutes) until the recording came back online.

Topics

  • Linear Models and the Least Squares Regression Line

Reading Assignment

  • Sections to Read Sections 7.1 - 7.2 in Introduction to Modern Statistics

  • Reading Questions (Submit answers on Gradescope)

    1. Suppose the residual of an observation is negative, based on a certain linear model. Does this mean the model over-estimated or under-estimate the true value of the outcome?

    2. A linear model to predict the cost of Reed tuition (in thousands of dollars) might be \[ \textrm{Cost} = 43 + 1.8 \cdot \textrm{Year} \] What do the values of the slope and intercept represent in the context of the model?

Week 4 Lab

Lab Demo

Topics

  • Linear Modeling (and some more dplyr practice)

Lab Assignment

Friday 2-18

Lecture Notes

Lecture Video

Topics

  • More on linear modeling

Reading Assignment

  • Sections to Read Chapter 5 Intro and sections 5.1 and 5.3 in ModernDive

  • Reading Questions (Submit answers on Gradescope)

    1. LC 5.1 (you don’t need to include your actual data or visualization, just your response to the question)

    2. What is the largest difference between the treatment of Linear Regression in ModernDive Section 5.1 and its treatment in Intro to Modern Statistics Section 7.1. i.e.What are you able to do after reading ModernDive that you weren’t able to do with just Intro to Modern Stat?

Homework Due

Homework is due by 11:59pm on Friday

Week 5

Monday 2-21

Lecture Notes

Lecture Video

Topics

  • Regression with categorical explanatory variables.

Reading Assignment

Note that the listed reading assignments should be completed prior to class

  • Sections to Read Section 5.2 in ModernDive

  • Reading Questions (Submit answers on Gradescope)

    1. In a linear regression model with quantitative response and categorical explanatory variable, why is there 1 fewer “slope” coefficients than there are levels of the categorical variable?
    2. LC 5.6
    3. What is one essential difference between regression models comparing 2 quantitative variables, and regression models comparing a quantitative and categorical variable?

Wednesday 2-23

Lecture Notes

Lecture Video

Topics

  • Multilinear Regression: One Categorical + One Quantitative Explanatory Variable

Reading Assignment

Note that the listed reading assignments should be completed prior to class

  • Sections to Read Section 6.1 in ModernDive

  • Reading Questions (Submit answers on Gradescope)

    1. What is one essential difference between the interaction model and the parallel slopes model for multiple linear regression?

    2. What is one conclusion we could draw from either the interaction or parallel slopes model for UT Austin evaluation scores in Section 6.1, that we could not draw from the simple linear model for UT Austin evaluation scores as a function of age (as in Section 5.1)?

Week 5 Lab

Lab Demo

Topics

  • Multiple Linear Regression

Lab Assignment

Friday 2-25

Lecture Notes

Lecture Video

Topics

Reading Assignment

Note that the listed reading assignments should be completed prior to class

  • Sections to Read Section 6.2 in ModernDive

  • Reading Questions (Submit answers on Gradescope)

    1. LC6.2 (You don’t need to include your data visualizations in your submission, just your answer to the question)

    2. Consider the following model for predicting a person’s weight (in kg) based on their height (in cm) and age (in years): \[ \hat{\textrm{Weight}} = -110 + 1 \cdot \textrm{Height} + 0.22 \cdot \textrm{Age} \]
    • Interpret the coefficient 0.22 in the context of this model.

Homework Due

Homework is due by 11:59pm on Friday

Week 6

Monday 2-28

Lecture Notes

Lecture Video

Reading Assignment

Note that the listed reading assignments should be completed prior to class

  • Sections to Read 7.1 and 7.2 in ModernDive

  • Reading Questions (Submit answers on Gradescope)

    1. LC 7.6, LC7.7

Wednesday 3-2

Lecture Notes

Lecture Video

Topics

Reading Assignment

Note that the listed reading assignments should be completed prior to class

  • Sections to Read 7.3, 7.5 in ModernDive

  • Reading Questions (Submit answers on Gradescope)

    1. LC 7.13, 7.15, 7.17

Week 6 Lab

Topics

  • Review for Midterm 1

Lab Assignment

Friday 3-4

Review Video

Topics

  • Review for Midterm 1

Reading Assignment

Note that the listed reading assignments should be completed prior to class

  • Sections to Read None

  • Reading Questions (Submit answers on Gradescope)

    1. Complete the “Practice with Timed Assignments” assignment on gradescope. Start by downloading this file Practice_with_Timed_Assignments_Template.Rmd and follow the instructions.

Homework Due

Homework is due by 11:59pm on Friday

Week 7

Monday 3-7

Lecture Notes

Lecture Video

Topics

  • The Bootstrap

Reading Assignment

Note that the listed reading assignments should be completed prior to class

  • Sections to Read 8.1 and 8.2 in ModernDive (This reading is optional, and will be revisited on Wednesday’s class)

  • Reading Questions (Submit answers on Gradescope)

    1. None

Wednesday 3-9

Lecture Notes

Topics

  • Introduction to Confidence Intervals

Reading Assignment

Note that the listed reading assignments should be completed prior to class

  • Sections to Read 8.3 in ModernDive (Review Sections 8.1 and 8.2 if you did not do so for Wednesday’s class)

  • Reading Questions (Submit answers on Gradescope)

    1. LC 8.1, 8.3

Week 7 Lab

Topics

  • Sampling and Bootstrapping

Friday 3-11

Lecture Notes

Lecture Video

Topics

  • More on Confidence Intervals

Reading Assignment

Note that the listed reading assignments should be completed prior to class

  • Sections to Read 8.4 and 8.5 in ModernDive

  • Reading Questions (Submit answers on Gradescope)

    1. What is one advantage offered by the infer package method for bootstrap confidence intervals compared to the “original workflow” discussed at the start of Section 8.4?

    2. Assuming that you have to use the same sample either way, which confidence interval has a higher certainty of containing the population parameter: a wider interval or a narrow interval? Explain.

Homework Due

Homework is due by 11:59pm on Friday

Week 8

Monday 3-14

Lecture Notes

Lecture Video

Topics

  • Hypothesis Testing Framework

Reading Assignment

Note that the listed reading assignments should be completed prior to class

  • Sections to Read 11.1 - 11.3 in Introduction to Modern Statistics

  • Reading Questions (Submit answers on Gradescope)

    1. In your own words, briefly explain what the null distribution for a test statistic represents.

    2. Suppose Nate has a coin that he flips repeatedly, recording the results each time. What type of evidence from a sequence of heads / tails would convince you that the coin is not fair?

Wednesday 3-16

Lecture Notes

Lecture Video

Topics

  • More on Hypothesis Testing

Reading Assignment

Note that the listed reading assignments should be completed prior to class

  • Sections to Read 9.1, 9.2 and 9.3 in ModernDive

  • Reading Questions (Submit answers on Gradescope)

    1. In the study on gender and promotion rate in Section 9.1, what are two possible explanations for the observed difference in promotion rate in the sample?

    2. LC 9.3

Week 8 Lab

Topics

  • Confidence Intervals and Hypothesis Testing in infer

Friday 3-18

Lecture Video

Reading Assignment

Note that the listed reading assignments should be completed prior to class

  • Sections to Read 9.4 - 9.6 in ModernDive

  • Reading Questions (Submit answers on Gradescope)

    1. LC 9.7, LC 9.8

Homework Due

Homework is due by 11:59pm on Friday

Spring Break

3/21 - 3/25

Week 9

Monday 3-28

Lecture Notes

Lecture Video

Topics

  • Axioms of Probability

  • Conditional Probability

Reading Assignment

Note that the listed reading assignments should be completed prior to class

  • Sections to Read Section 3.1 and 3.2 in THIS EXCERPT from OpenIntro Statistics Note: This is neither the ModernDive textbook nor the Intro to Modern Statistics textbook.

  • Reading Questions (Submit answers on Gradescope)

    1. Briefly explain why the following situation is not a contradiction of the Law of Large Numbers:

“A fair coin is flipped 10 times and lands heads each time.”

  1. Suppose a fair coin is flipped 10 times. What is the probability that all 10 flips are heads? What is the probability that either all 10 flips are heads or all 10 flips are tails?

  2. Suppose a fair coin is flipped twice. What is the conditional probability that the second flip is a heads given that neither flip is tails?

Wednesday 3-30

Lecture Notes

Lecture Video

Topics

  • Random Variables

Reading Assignment

Note that the listed reading assignments should be completed prior to class

  • Sections to Read Section 3.4 - 3.5 in THIS EXCERPT from OpenIntro Statistics Note: This is neither the ModernDive textbook nor the Intro to Modern Statistics textbook.

  • Reading Questions (Submit answers on Gradescope)

    1. In your own words, describe the difference between a quantitative variable and a random variable.

    2. Give an example of a random process you think could be well-represented by a discrete random variable. Give an example of a different random process you think could be well-represented by a continuous random variable.

    3. Suppose we model the length of a randomly selected earthworm as a continuous variable with mean 14 inches. What is the probability that the length of a randomly selected earthworm is exactly 14 inches? Explain.

Week 9 Lab

Lab Video

Topics

  • Probability and Simulation

Friday 4-1

Lecture Notes

Lecture Video

Topics

  • The Central Limit Theory and Probability Models

Reading Assignment

Note that the listed reading assignments should be completed prior to class

The Quincunx, bean machine, or ``Galton Board’’ was invented by 19th century English scientist Sir Francis Galton to demonstrate fundamental principles in probability and statistics. In its basic form, the Quincunx consists of an upright triangular board with evenly spaced pegs lying above evenly spaced bins. Balls are dropped one-by-one from a central chute at the top of the board and bounce either left or right as they hit the pegs. Eventually, they are collected in the bins at the bottom of the board.

Spend some time playing around with the Galton Board here. (After you adjust sliders, be sure to hit the “restart” button as well.)

  1. Viewing the stacks of balls at the bottom of the board as a histogram, what named distribution is the histogram similar to?

  2. What effect does increasing the size slider have on the shape of the histogram? What effect does increasing the Left/Right slider have on the shape?

  3. What effect does increasing the Speed slider have on the shape?

  4. During which time interval will the shape of the histogram change more? (a) between the 1st and the 100th balls, or (b) between the 901st and 1000th balls? Explain.

Homework Due

Homework is due by 11:59pm on Friday

Week 10

Monday 4-4

Lecture Notes

Topics

  • The Central Limit Theory and Probability Models

Reading Assignment

Note that the listed reading assignments should be completed prior to class

Wednesday 4-6

Notes for Class

Topics

  • A Preview of Upcoming Statistics Classes

Reading Assignment

Note that the listed reading assignments should be completed prior to class

  • Sections to Read None

  • Reading Questions (Submit answers on Gradescope)

    1. None

Week 10 Lab

Topics

  • The Central Limit Theorem and Normal Distributions

Friday 4-8

Lecture Notes

Lecture Video

Topics

  • Inference for Proportions

Reading Assignment

Note that the listed reading assignments should be completed prior to class

  1. Suppose you are interested in determining whether a majority of Americans disapprove of the US president. In a simple random sample of 100 Americans, you find that 60% disapprove of the current president, which gives a p-value of 0.02, and leads you to reject the null hypothesis. Explain what this means in everyday language in context of this problem.

  2. Suppose we want to construct a confidence interval for a population proportion \(p\). Based on the Central Limit Theorem, the standard error of the sample proportion \(\hat p\) is \[ SE(\hat p) = \sqrt{\frac{p(1-p)}{n}} \] Explain why we cannot directly apply this formula to create the confidence interval for \(p\).

Homework Due

Homework is due by 11:59pm on Friday

Week 11

Monday 4-11

Lecture Notes

Lecture Video

Topics

  • Inference comparing two proportions

Reading Assignment

Note that the listed reading assignments should be completed prior to class

  • Sections to Read 17.3 in Introduction to Modern Statistics

  • Reading Questions (Submit answers on Gradescope)

    1. In order to perform hypothesis testing or create confidence intervals based on a difference in sample proportions \(\hat p_1 - \hat p_2\), we need to check 2 conditions. What are those conditions?

    2. Suppose you perform two 2-sided hypothesis tests for a difference in proportion. In the first test, you obtain a test statistic of \(z = -2.05\) and in the second test, you obtain a test statistic of \(z = 0.04\). Which test gives better evidence to reject the null hypothesis? Explain.

Wednesday 4-13

Lecture Notes

Lecture Video

Topics

  • The \(t\)-distribution and inference for a single mean

Reading Assignment

Note that the listed reading assignments should be completed prior to class

  • Sections to Read 19.2 in Introduction to Modern Statistics

  • Reading Questions (Submit answers on Gradescope)

    1. Describe at least 1 similarity and 1 difference between a t distribution and the standard Normal distribution.

    2. Suppose you are interested in investigating the typical course load for Reed students. You obtain a random sample of 25 Reed students and record the number of credits each is currently taking as the variable credits. If you want to perform inference using the credits variable, is the parameter of interest a mean or a proportion? Explain how you know.

Week 11 Lab

Topics

  • Theory-based Inference for Means and Proportions

Friday 4-15

Lecture Notes

Lecture Video

Topics

  • Inference for difference in means

Reading Assignment

Note that the listed reading assignments should be completed prior to class

  • Sections to Read 20.3, 20.4, 21.3 in Introduction to Modern Statistics

  • Reading Questions (Submit answers on Gradescope)

    1. A study wishes to determine whether automatic and manual transmission cars have the same fuel efficiency. They randomly select 10 automatic cars and 10 manual cars, and measure number of gallons of gas consumed by each after a 100 mile trip. Write null and alternative hypotheses for this research question, both in words and in symbols.

    2. Consider the following two experiments. Which has paired design and which corresponds to two independent samples? Explain how you know.

    1. Does marijuana assist in injury recovery? A randomized experiment assigns subjects with sprained ankles into two groups: 10 receive a THC brownie every evening for 14 days, while another 10 receive an ordinary brownie every evening for the same period. The number of days until symptoms disappear is recorded for each subject.

    2. A campus organization wants to determine whether listening to rock music before bed has an effect on length of sleep. They recruit 20 students and have them track the number of hours they sleep each night over a 14 day period. After these two weeks, the organization then instructs each of the 20 students to listen to rock music for 1 hour each night before going to sleep, and track the number of hours they get each night over a 14 day period. The organization records the average number of hours each student sleeps with and without rock music.

Homework Due

Homework is due by 11:59pm on Friday

Week 12

Monday 4-18

Lecture Notes

Lecture Video

Topics

  • Inference for Simple Linear Regression

Reading Assignment

Note that the listed reading assignments should be completed prior to class

  • Sections to Read 24.1 - 24.6 in Introduction to Modern Statistics

  • Reading Questions (Submit answers on Gradescope)

    1. Consider two quantitative variables measured on a population of students: length of index finger and height. If these two variables are independent, and we repeatedly draw samples of 25 students from the population, computing the regression line for each, what do you anticipate will be the average slope for the regression line?

    2. The scatterplot, residual plot, and histogram of residuals for variables \(Y\) and \(X\) are shown below. Discuss any concerns you might have about whether the data satisfies the conditions for making inference about linear regression, based on these plots.

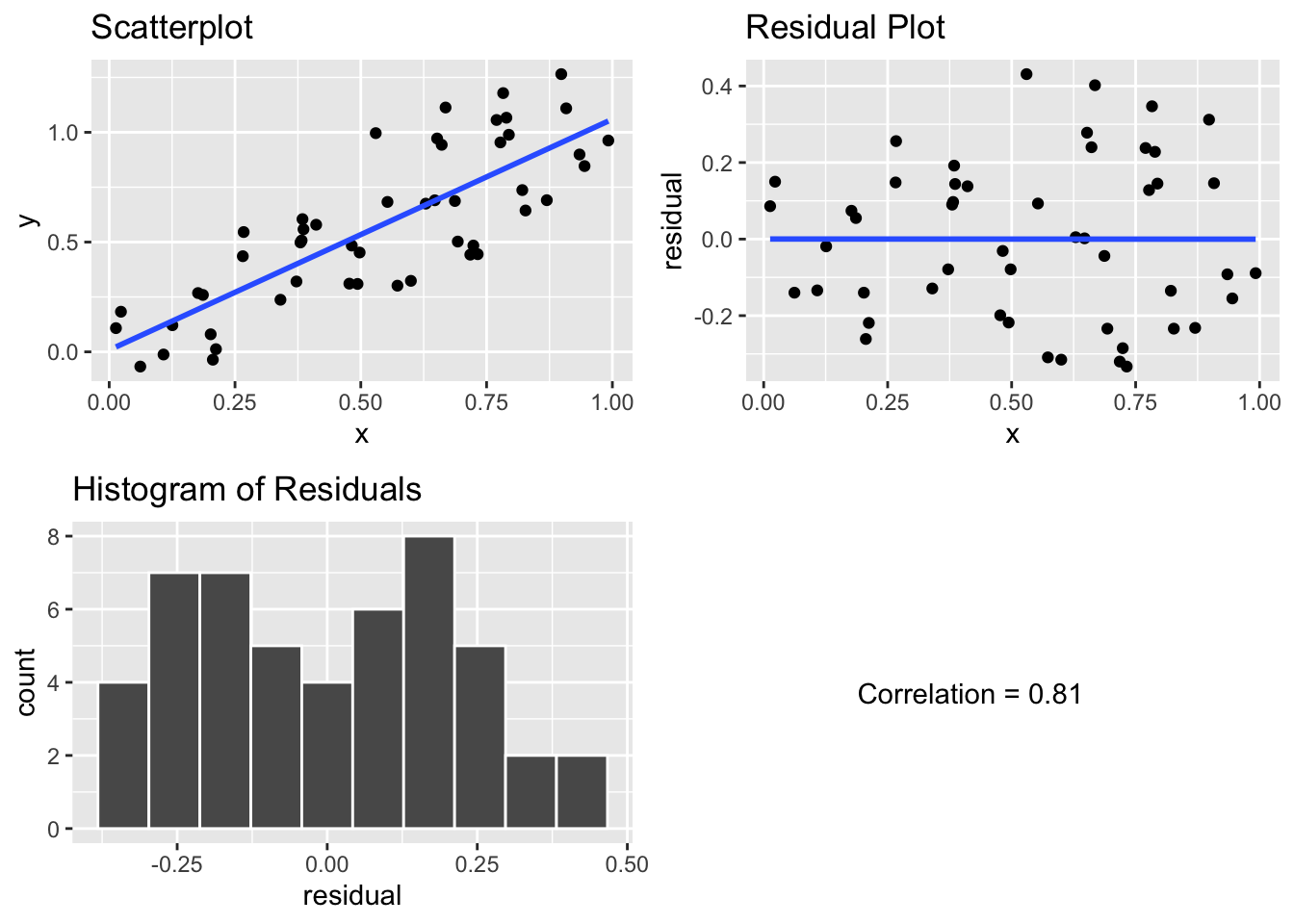
Wednesday 4-20

Lecture Notes

Lecture Video

Topics

  • Inference for MLR

Reading Assignment

Note that the listed reading assignments should be completed prior to class

  • Sections to Read 25.1, 25.2, 8.3, 8.4 in Introduction to Modern Statistics

  • Reading Questions (Submit answers on Gradescope)

    1. Suppose we are interested in predicting college GPA based on high school GPA and SAT scores. We construct to linear models. The first model is of the form \[ \textrm{college GPA} = \beta_0 + \beta_1 \textrm{HS GPA} \] and the second model is of the form \[ \textrm{college GPA} = \beta_0 + \beta_1 \textrm{HS GPA} + \beta_2 \textrm{SAT} \] Suppose we wish to perform a hypothesis test for the slope on \(\textrm{HS GPA}\) in the two models. State the null hypothesis in each case, and explain the fundamental way in which these two hypotheses differ.

    2. Based on the discussion in Section 8.3 and 8.4, what is one reason we may decide to use parsimonious model over the full model?

Week 12 Lab

Discussion Video

Topics

  • Inference for Linear Regression

Friday 4-22

Lecture Notes

Lecture Video

Topics

  • Multilinear Regression Models

Reading Assignment

Note that the listed reading assignments should be completed prior to class

  • Sections to Read Review 25.1, 25.2, 8.3, 8.4 in Introduction to Modern Statistics (This was Wednesday’s reading)

  • Reading Questions (Submit answers on Gradescope)

    1. None

Homework Due

Homework is due by 11:59pm on Friday

Week 13

Monday 4-25

Lecture Notes

Lecture Video

Topics

  • ANOVA

Reading Assignment

Note that the listed reading assignments should be completed prior to class

  • Sections to Read 22.1 - 22.3 in Introduction to Modern Statistics

  • Reading Questions (Submit answers on Gradescope)

    1. Suppose you are interested in knowing whether a certain date in April is associated with higher than average number of births. To answer this question, you look at the average number of births for each of the 30 days, based data from 100 hospitals, and find that on April 23rd, there is a statistically significant difference at the 5% level in the number of births compared to the overall average. Explain why it would be incorrect to conclude that this gives good evidence that in general, there are more births on average on April 23rd? (Think about how many different tests you are performing at the 5% level)

    2. Consider the 3 sets of boxplots shown below. Which set gives the strongest evidence of a difference in means? Explain. Solid red dots in each box represent the means for each group

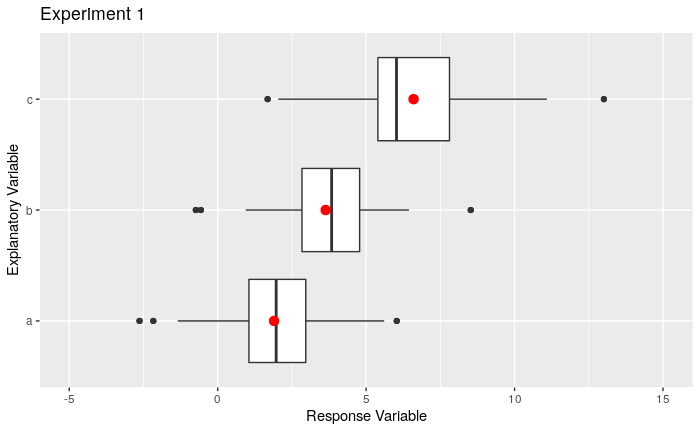
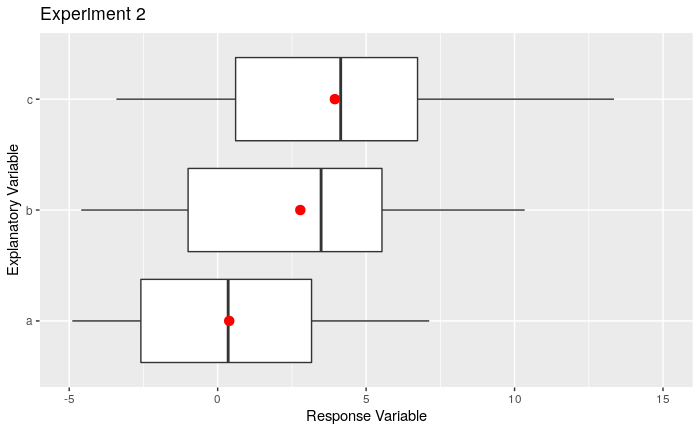
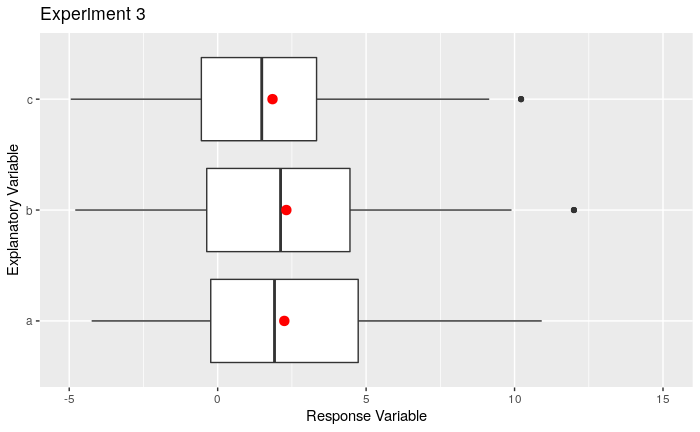
Wednesday 4-27

Lecture Notes

Lecture Video

Topics

  • Chi-Square Tests

Reading Assignment

Note that the listed reading assignments should be completed prior to class

  • Sections to Read 18.1 and 18.2 in Introduction to Modern Statistics

  • Reading Questions (Submit answers on Gradescope)

    1. Describe 1 similarity and 1 difference between the Chi-Squared Test for Independence and the Hypothesis Test for Difference in 2 Proportions.

    2. Consider 2 sections of Math 141. In total, 20% of students are first years, 30% of students are sophomores, 40% of students are juniors, and 10% of students are seniors. If section and year in school are independent, and there are 20 students in the 10am section of Math 141, what are the expected number of 1st Years, Sophomores, Juniors, and Seniors in the 10am section?

Week 13 Lab

Topics

  • ANOVA and Multilinear Regression

Friday 4-29

Lecture Notes

Lecture Video

Topics

  • Review

  • Course Summary

Reading Assignment

Note that the listed reading assignments should be completed prior to class

  • Sections to Read None

  • Reading Questions (Submit answers on Gradescope)

    1. None. But if you haven’t completed your course evaluations, please do so.

Homework Due

Homework is due by 11:59pm on Friday